Long Short-Term Memory (LSTM)

LSTM은 vanishing or exploding gradient problem와 long term dependency를 개선한 모델이다.
초반 정보(단기 기억)를 후반(장기 기억)까지 끌고 가기 위해 개선했기에 Long Shot-Term이라는 이름이 붙었다.
기존 RNN의 수식을 h_t = f_W(x_t, h_t-1)라고 표현한다면,
LSTM의 수식은 (C_t, h_t) = LSTM(x_t, C_t-1, h_t-1)라고 표현한다.
이때 C_t는 cell state vector라고 부르며, RNN의 hidden state vector에 해당한다.
위의 그림으로는 A 영역에 2개의 화살표가 나와서 다시 A 영역으로 들어가는데, 위의 화살표가 C_t에 해당한다.
핵심 정보를 포함하는 벡터는 C_t에 해당한다.
LSTM에서 h_t 벡터는 C_t를 한 번 더 가공하여, 현재 step에서 필요로 하는 정보만을 담은 filtering한 벡터이다.

LSTM의 내부 동작 과정을 살펴보자.
LSTM의 세 가지 입력 x_t, c_t, h_t-1 중 먼저 x와 h만을 받아서 계산을 수행한다.
x와 h를 가중치 행렬 W에 곱한 뒤, 4개의 그룹으로 나누어 각각 sigmoid 혹은 tanh 연산을 수행한다.
4개의 그룹 중 3개의 그룹에는 sigmoid 연산을, 1개의 그룹에만 tanh 연산을 수행한다.
활성화 함수(activation function) 연산 이후에 나오는 결과를 'Ifog 게이트'라고 부른다.
| 게이트 | 명칭 | 설명 |
| I | Input Gate | Cell에 쓸지 말지를 결정하는 게이트 들어오는 input에 대해서 마지막 sigmoid를 거쳐 0 ~ 1 사이로 표현한다. 이 값은 cell state와 hidden state 두 갈래로 흘러간다. |
| F | Forget Gate | 정보를 얼마나 지울지 0 ~ 1 사이로 표현한다. |
| O | Output Gate | Cell 정보를 hidden state에서 얼마나 사용할지를 0 ~ 1 사이로 표현한다. |
| G | Gate gate | Cell state에 얼마나 반영할지를 -1 ~ 1 사이로 표현한다. Vanilla RNN에서 사용한 것과 같이 중요 정보를 담는 벡터라고 할 수 있다. |
게이트 설명은 위와 같다.
일반적으로 4개의 게이트는 이전 step의 cell state vector를 변환할 때 사용한다.
장기 기억을 유지하기 위해 cell state와 gate를 추가한 구조를 사용하는 것이다.
가령 Ct-1 벡터가 3차원 벡터라고 가정하고, ifog의 사용을 살펴보자.
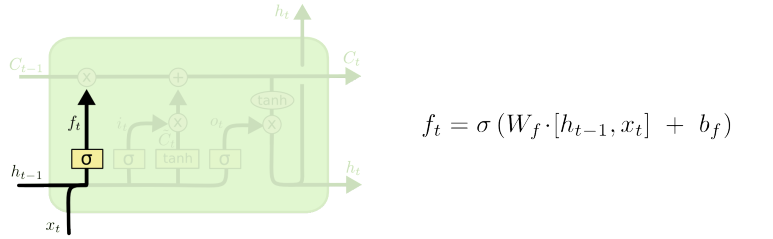
Forget gate는 이후 들어올 C_t-1 벡터의 일부 정보만을 남게 한다.
활성화 함수가 sigmoid라면 최소가 0 최대 1이기 때문에 0.xx의 비율로 값이 나오게 된다.
즉 C_t-1 벡터를 특정 비율만큼 지우는 gate이기에 forget gate라고 부른다.

첫 번째 문단에서 언급했던 것처럼 LSTM의 C_t는 Vanilla RNN의 h_t에 해당한다.
즉 C̃t는 LSTM이 현재 정보(x_t)와 이전 출력(h_t-1)을 가지고 계산한 새로운 cell state vector이다.
이것을 계산하는 것이 gate gate이다.
새로운 cell state vector를 전부 반영하면 좋겠지만, 그랬다가는 장기 기억에 문제가 발생한다.
따라서 forget gate처럼 cell state vector를 현재 셀 상태에 얼마나 반영할지 결정해야 한다.
즉 sigmoid 활성화 함수를 통과한 input gate로 생존 비율을 정해줘야 한다는 말이다.
Forget gate와 수식은 같지만, 새로운 vector를 어느 비율로 살려서 넣을 것이냐는 측면에서 input gate라고 부른다.
Input gate는 새로운 정보를 현재 셀 상태(C_t)에 추가할지 말지를 정한다.

위 두 과정에서 얻은 forget gate, gate gate, input gate를 사용하여 C_t-1를 갱신한다.
수식을 보면 가중치(W)를 계속해서 곱하는 연산이 아니라, forget gate를 거친 값과 input gate를 거친 값.
2가지 값의 덧셈을 통해 연산하기 때문에, 필요로 하는 정보만을 취하게 된다.
이 방식을 통해 gradient problem을 방지한다.
수식을 이해하기 편하게 말로써 풀어서 쓰면, '이전 상태의 일부분과 현재 상태의 일부분을 더한다'가 된다.
해당 과정을 통해 얻은 C_t는 장기 기억에 속한다.
이렇게 cell state vector의 갱신은 끝난다.
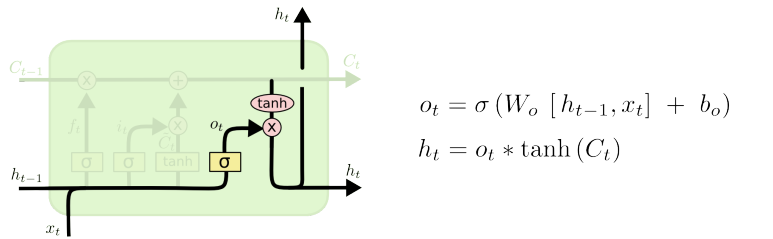
LSTM의 cell state 연산은 끝났으니, 이제 hidden state를 구해야 한다.
위에서 구한 C_t에 tanh 함수를 적용하여 범위를 -1에서 1 사이로 만들어준다.
그 후 시그모이드를 통해 계산한 output gate를 곱해주어 forget, input과 마찬가지로 일부만을 살린다.
맨 위에서 언급한 "LSTM에서 h_t 벡터는 C_t를 한 번 더 가공하여, 현재 step에서 필요로 하는 정보만을 담은 filtering한 벡터이다 "에 해당하는 연산이다.
즉 해당 과정을 통해 얻은 h_t는 단기 기억에 속한다.
현재 step에서 필요로 하는 정보만을 담는 이유는, h_t 벡터는 2가지 이유로 쓰인다.
첫 번째는 다음 time step으로 전달하여 장기 패턴 학습을 위해 사용하고,
두 번째는 현재 시점의 예측값을 위해 출력층(output layer) 로 전달해야 하기 때문이다.
첫 번째 이유처럼 장기 패턴을 학습하기 위해서는, 시그모이드 연산이 필요하다.
이렇게 시그모이드 연산을 하는 이유는 셀 상태(C_t)가 너무 강한 영향을 주는 것을 방지하기 위함이다.
지금 계산한 C_t는 장기 기억을 저장하는 벡터이다.
해당 정보를 그대로 사용한다면 모델의 유연성이 떨어질 수 있기에, 은닉층에서 동적으로 조절하는 것이 필요하다.
Gated Recurrent Unit(GRU)

GRU는 LSTM 모델 구조를 경량화하여, 적은 메모리로 빠른 계산이 가능하게끔 만든 모델이다.
GRU의 가장 큰 특징은, 2가지 상태로 존재하던 cell state vector와 hidden state vector를 일원화한 점이다.
c_t와 h_t가 모두 존재하는 게 아닌, h_t(hidden state) 하나만이 존재한다는 것이다.
이때 장기 기억을 가진다는 측면에서, GRU의 h_t는 LSTM의 c_t와 역할이 비슷하다.
또한 LSTM에서는 input gate와 forget gate를 사용했지만,
GRU에서는 forget gate를 따로 두지 않고, (1 - input gate)의 값을 사용한다.
└ 가중 평균을 사용한다는 말과 같다.
└ GRU에서 input gate는 z_t에 해당한다.

위 사진은 LSTM, GRU의 backpropagation 갱신 과정이다.
가중치를 계속해서 곱하는 Vanilla RNN과 달리, time step마다 다른 forget gate를 곱하고 필요한 정보를 덧셈으로 만든다.
이를 통해 vanishing or exploding gradient problem을 해소했다.
기본적으로 backpropagation을 할 때 덧셈 연산은 gradient를 복사해주는 역할을 한다.
멀리 있는 time step까지 큰 변형없이 전달이 가능하고, 긴 time step간의 long term dependency를 해결한다.
└ Gradient problem은 역전파 학습 중에 발생하는 기울기가 극단적으로 변하는 문제
└ Long term dependency는 학습 모델이 장기 정보를 유지하지 못 해, 과거 정보가 현재 예측에 영향을 주기 어려운 문제
'공부 > BoostCourse 자연어 처리' 카테고리의 다른 글
| 10. Seq2Seq - Attention Mechanisms (0) | 2025.03.17 |
|---|---|
| 09. Seq2Seq - Model (0) | 2025.03.14 |
| 07. NLP DL - Backpropagation through time and Long-Term-Dependency (0) | 2025.03.12 |
| 06. NLP DL - Character-level Language Model (0) | 2025.03.11 |
| 05. NLP DL - Recurrent Neural Network (RNN) (0) | 2025.03.10 |
