프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
백준 문제를 매일 풀다가 문득 생각이 들었다.
코딩 테스트를 통과하기 위해서 알고리즘 문제를 열심히 풀고 있다.
하지만 이건 '강한 상대를 이기기 위해 수련을 한다'와 같은 맥락이지 않을까?
강한 상대를 이기기 위해 수련한다고? 웃기는 말이다.
나보다 강한 상대를 이기기 위해서는, 나보다 강한 상대에게 계속 도전하는 것밖에 없다.
알고리즘을 공부하는 게 나쁜 건 아니지만, 내 목표는 코딩 테스트 통과다.
그러기 위해서는 실제 코딩 테스트 문제를 많이 풀어보는 게 도움이 더 되리라 생각했다.
그래서 2023 KAKAO BLIND 문제 풀이에 다시 도전했다.
이미 LV1과 LV2의 세 문제는 모두 풀었었기에, LV3 문제에 도전했다.
바로 "표현 가능한 이진트리" 문제다.
2023 KAKAO BLIND 표현 가능한 이진트리
1번 문제가 완료한 사람 11960명에 정답률 42%인 것에 비해
4번 문제는 완료한 사람 1930명에 정답률 28%밖에 되지 않는다.
문제가 어려울 것이라 생각했는데, 문제 자체를 이해하는 것은 쉽다.
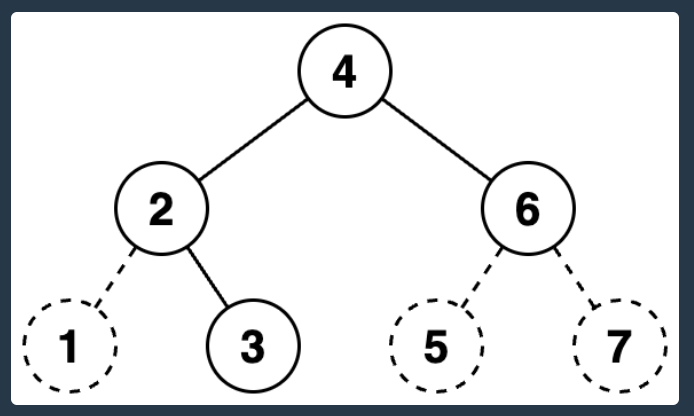
핵심은 두 번째 그림이다.
실선으로 연결된 부분은 1, 점선으로 연결된 부분은 0이다.
이때 왼쪽에서부터 오른쪽으로 순서대로 읽는다면 0111010이다.
111010을 10진수로 나타내면 58이 되니까, 58은 이진트리로 표현할 수 있는 숫자다.
그럼 왼쪽에서 오른쪽으로 읽을 때, 어떤 노드 순서대로 읽어야 할까?
"이진트리에서 리프 노드가 아닌 노드는 자신의 왼쪽 자식이 루트인 서브트리의 노드들보다 오른쪽에 있으며, 자신의 오른쪽 자식이 루트인 서브트리의 노드들보다 왼쪽에 있다고 가정합니다. "라고 쓰여있다.
조금씩 끊어서 읽으면 쉽다. 그냥 전위순회 순서대로 판단합니다~라는 뜻이다.
난이도와 정답률에 비해서는 문제가 쉬울 수도 있다는 생각을 했다.
특정 이진트리를 그려라!가 아니라 이 숫자가 이진트리가 되는가?를 묻는 문제라서 더 그렇다.
그럼 주어진 숫자를 2진수로 바꾸고, 이진트리가 되는지만 확인하면 되는 거 아닌가.
문제 조건에서 "포화 이진트리"라고 했으니, 왼쪽에 0을 패딩하면 된다.
포화 이진트리를 전위순회한다면, 리프 노드의 index는 (1부터 시작한다면) 반드시 홀수다.
그럼 짝수 입장에서, 0일 때 자식 노드가 1이 아니기만 하면 되는 문제 아닌가?
이진트리, 0과 1, 2진수 연산 ... 어? 이거 비트마스킹으로 풀 수도 있겠는데?
단순하게 생각하면 리프노드에 닿을 때까지 이분 탐색을 하든, 재귀 호출을 하든 될 것 같았다.
하지만 비트마스킹이 되겠는데? 짝수 index만 확인하면 되겠는데?라는 생각이 들자,
풀이 방법이 그쪽으로 가속이 붙기 시작했다. 그래서 이번 문제는 비트마스킹을 이용한 도전을 했다.
bnum = bin(num)[2:]
len_bin = len(bin(num)[2:])우선 2진수로 값을 바꿔야 이진트리를 그리든 말든 할 수 있다.
그래서 2진수 숫자(bnum)을 내장 함수 bin()을 이용하여 구한다.
앞에 0b 식별자를 제거하기 위해 2번째 index부터 slicing한다. bin()의 return값이 str이라 가능하다.
그리고 bnum의 길이(현재 노드가 몇 개인지)를 구해준다.
next_squ2minus1 = 2 ** (len(bin(len_bin)[2:])) - 1위의 코드가 바로 다음 포화 이진트리를 찾는 코드이다.
작성한 코드에서 핵심이 되는 코드다.
len_bin에는 2진수로 바꿨을 때의 길이가 들어있다. 즉 현재 사용하고 있는 노드의 개수와 동일하다.
2진수가 1011이라면, len_bin에는 4를 저장한다.
2진수가 101010이라면, len_bin에는 6을 저장한다.
현재 노드 개수가 포화 이진트리만큼 필요하다면, (2의 거듭제곱 - 1)개만큼 필요하다.
이를 구하기 위해서는 길이를 한 번 더 2진수로 바꿔주면 된다.
예를 들어서 len_bin(현재 노드) 개수가 6이라고 가정해보자.
그럼 6에 (증가하는 방향으로) 가장 가까운 2의 거듭제곱은 8이다.
즉, 포화 이진트리가 되기 위해서는 8 - 1 = 7로 7개가 필요하다. 이를 위해 2진수로 접근해보자.
6은 2진수로 110이다. 포화 이진트리가 되기 위해서는 모든 0을 1로 바꾸면 된다.
(2 ** num) - 1
num개의 비트를 모두 1로 켜는 비트마스킹을 응용했다.
110이라는 자릿수를 모두 1로 만들기 위해서는, 자릿수가 필요하다.
자릿수는 노드 개수를 2진수로 바꾼 뒤, 그 길이를 세는 것과 동일하다.
len_bin을 bin() 함수에 씌운 뒤, len()으로 길이를 센다는 말이다.
fill = bnum.zfill(next_squ2minus1)
rev_fill = fill[::-1]이제 가장 처음 구한 2진수 bnum을 next_squ2minus1 개수만큼 0으로 패딩하면 된다.
파이썬에서는 zfill() 내장 함수로, 문자열 앞부분에 원하는 자릿수가 될 때까지 0으로 채워준다.
rev_fill은 fill을 1부터 (낮은 자릿수부터) 세기 위해서 뒤집어서 저장했다.
for idx, val in enumerate(rev_fill):
if idx % 2 == 1 and val == "0":
bef_idx = idx - 1
aft_idx = idx + 1
if int(rev_fill[bef_idx]) + int(rev_fill[aft_idx]):
return 0
return 1이제 0과 1로 채운 포화 이진트리를 만들었으니, 실제로 있을 수 있는지 확인할 차례다.
위에서 설명했듯 (1부터 센다면) 리프 노드의 index는 홀수다.
하지만 0부터 세주었기 때문에, 위 코드에서 리프 노드의 index는 짝수에 해당한다.
즉, 짝수 노드는 검사할 필요가 없다는 말이다.
부모 노드가 0일 때, 자식 노드가 1이 없기만 하면 된다.
반복문으로 돌면서 리프 노드가 아니면서(idx % 2 == 1), 값이 0일 때(val == "0") 확인한다.
예를 들어서 2번째 노드가 값이 0인데, 1번째나 3번째 노드가 1로 존재할 수 없다.
그래서 bef_idx와 aft_idx에 현재 idx에 1을 더하거나 빼서, 바로 밑에 자식 노드를 확인한다.
두 노드 값을 더했을 때 True라면 어디든 값이 하나라도 존재한다는 말과 같다.
따라서 그런 경우 바로 return 0 하여 함수를 빠져나온다.
모든 리프가 아닌 노드를 돌면서 전부 성립한다면 return 1로 빠져나오면 된다.
def solution(numbers):
def proof(num):
bnum = bin(num)[2:]
len_bin = len(bin(num)[2:])
# Test Code
# squ2minus1 = int(len_bin) & (int(len_bin)+1)
# is_squ2minus1 = False if squ2 else True
next_squ2 = 2 ** (int(len(bin(len_bin)[2:]))) - 1
fill = bnum.zfill(next_squ2)
reverse_fill = list(fill[::-1])
for idx, val in enumerate(reverse_fill):
if idx % 2 == 1 and val == "0":
minus_idx = idx - 1
plus_idx = idx +1
if int(reverse_fill[minus_idx]) + int(reverse_fill[plus_idx]):
return 0
return 1
answer = []
for num in numbers:
answer.append(proof(num))
return answer최종적으로 제출한 코드는 위와 같다.
절반 이상이나 틀렸다.
한두 개만 틀렸다면 1이나 2, 아니면 10^15 같은 극단적인 경우에 틀렸다고 보통 유추할 수 있다.
하지만... 절반 이상이 틀린다는 건, 이 알고리즘이 맞다고 확신해도 어딘가 분명 틀린 게 있다는 거다.
우선 틀린 부분을 찾아내기 전에 코드가 조금 복잡하다고 생각되어 정리를 해주었다.
next_squ2minus1 = 2 ** (len(bin(len_bin)[2:])) - 1
next_squ2minus1 = (1 << (len(bin(len_bin)[2:]))) - 1위에서 비트마스킹을 응용하여 자릿수를 모두 켜줬다고 했다.
하지만 2의 거듭제곱이 아니라 진짜 비트마스킹을 쓰면 된다.
위의 상단 코드에서 하단 코드로 변경해주었다. 둘 다 같은 코드다.
fill = bnum.zfill(next_squ2minus1)
# 제거: reverse_fill = list(fill[::-1]) next_squ2minus1자리만큼 0으로 패딩을 한 fill 문자열 변수다.
낮은 자리부터 확인하기 위해서 역순으로 정렬한 reverse_fill을 선언했었다.
하지만 높은 자리부터하나 낮은 자리부터하나 차이가 없다.
reverse_fill은 지우고 fill로 반복문을 진행하게 했다.
여러 숫자들을 시도하던 중 96이라는 숫자를 발견했다. (나중에보니 질문 게시판에도 같은 숫자가 있었다.)
위의 그림이 헷갈릴 수 있겠지만, 검은색은 포화 이진트리 구조고, 빨간색이 들어있는 숫자다.
96이라는 숫자는 2진수로 바꾸면 1100000이 된다. 그걸 문제처럼 바꾸면 위의 구조가 되고.
이때 2번째 노드 입장에서는 문제가 없다.
본인이 1이기 때문에 자식 노드에는 1이 있든말든 상관이 없다.
여기서 작성한 코드에 2가지 문제를 발견했다.
하나, 우선 바로 직전 index와 바로 직후 index가 올바르게 가리키지 않는다.
루트 노드 입장에서 자식 노드를 확인해야 하는데, 파란색으로 가리킨 노드를 확인한다.
둘, 바로 밑 자식 노드가 아니라 더 밑의 자식 노드도 확인해야 한다.
그림으로 살펴보자.
8의 입장에서 4와 12만 검사해도 된다고 생각했다.
하지만 8, 4, 12가 전부 0인데, 갑자기 6 값이 1이라면? 8 입장에서는 잡아내지 못한다.
바로 다음의 자식 노드만 확인할 것이 아니라, 자식 노드의 모든 범위를 검사해야 한다.
포화 이진트리가 작아서 그렇지, 범위가 커진다면 어디서 예외가 발생할지 모른다.
그래서 정확하게 범위를 잡아줘야 한다고 생각했다.
어떻게 범위를 잡아줘야 할까 고민한 흔적이다.
그렇게 공통점을 찾아보다가, '첫 번째로 나오는 하위 1bit'가 핵심임을 찾았다.
예를 들어 4번째 노드는 1부터 7까지 탐색을 해야 한다.
4에서 첫 번째로 나오는 하위 1bit는, 100에서 2^2에 해당하는 1이다.
즉 000 세자리에 해당하는 범위를 검사하면 된다는 말이다.
그럼 10은 어떨까? 10번째 노드는 9부터 11까지 탐색을 해야 한다.
10에서 첫 번째로 나오는 하위 1bit는, 1010에서 2^1에 해당하는 1이다.
즉 00 두 자리에 해당하는 범위를 검사하면 된다. 나머지 상위 비트는? 범위에다 더해주면 된다.
10을 2진수로 바꾸면 1010이고, 검사할 범위는 00 두자리다.
그럼 영향을 받지 않는 bit는 1000이라고 할 수 있다.
00 두 자리의 최솟값은 01, 최댓값은 11이다.
영향을 받지 않는 1000에 최솟값과 최댓값을 더하면 실제로 검사할 범위가 된다.
1000 + 01 = 1001 = 9
1000 + 11 = 1011 = 11
fir_bin = idx & (-idx)문제는 하위 1bit를 어떻게 찾느냐다.
반복문으로 찾았다가는 시간복잡도가 증가하여 시간 안에 풀지 못 할 것 같았다.
이 역시도 비트마스킹을 활용
비트 A가 있다고 하자. 또한 A의 최소 원소(가장 오른쪽의 1)를 k라고 하자.
그럼 k가 1이라면, k를 기준으로 오른쪽의 모든 비트(0 ~ k-1)는 0이다.
~A를 하면 k는 0이 되고, 0부터 k-1까지의 비트는 모두 1이다.
~A + 1을 하면 k는 다시 1이 되고, 0부터 k-1까지의 비트는 모두 0이다.
A와 (~A + 1)을 AND(&) 연산하면, k를 기준으로 상위 비트는 NOT(~) 연산에 의해 모두 0이 된다.
그리고 k를 기준으로 하위 비트는 ~A+1에서 0이므로 AND(&)에서 모두 0이 된다.
즉 k 비트만이 켜진 상태로 남는다.
이산수학에서 배운 보수 표현에 대해 익숙하다면 한 가지가 보일 것이다.
~A + 1은 컴퓨터가 표현하는 A의 2의 보수(-A)다.
결과적으로 A에서 최소 원소를 찾는 연산은 A & (-A)가 된다.
fir_bin_idx = len(bin(fir_bin)[2:]) - 1
rem_bin = idx & ~(1 << fir_bin_idx)최소 원소(하위 1비트)를 찾았으니, 그걸 기준으로 나눌 차례다.
fir_bin에 최소 원소 값을 저장했으니 index도 찾아야 한다.
예를 들어 10100이라면 fir_bin에는 4가 저장된다.
len()과 bin()을 조합하여 길이를 잰 뒤, index는 0부터 시작하기 때문에 1을 빼주었다.
remain 변수에는 AND(&)와 NOT(~) 비트마스킹을 조합하여 하위 비트를 모두 꺼주었다.
bef_idx = rem_bin # 1 + rem_bin - 1
aft_idx = ((1 << fir_bin_idx+1) - 1) + rem_bin위에서 잠깐 언급했듯, 몇 자리가 됐든지 가장 작은 값은 1이다.
1에 rem_bin을 더하면 최솟값의 범위가 된다.
하지만 index는 1을 뺴줘야 하기 때문에, 실질적인 bef_idx 값은 rem_bin 자체가 된다.
가장 큰 값은 자릿수만큼 모든 비트를 켜주고, rem_bin을 더하면 된다.
위에서 구한 fir_bin_idx는 인덱스 값을 저장했기 때문에 1을 뺐었다.
하지만 인덱스가 아닌 개수를 구하기 위해서는 다시 1을 더해줘야 한다(fir_bin_idx+1).
(1 << num) - 1을 하면 num 개수만큼 1비트가 켜지기 때문이다.
마지막으로, 파이썬에서 Slicing을 할 때 뒤의 범위는 포함하지 않기 때문에 굳이 -1을 할 필요가 없다.
if any(int(i) for i in fill[bef_idx:aft_idx]):
return 0Generator expression을 이용하여 조금이라도 시간을 단축하려고 했다.
bef_idx부터 aft_idx까지 모든 요소를 돌면서 하나라도 1이 나오는 순간 멈추고 return 0을 한다.
def solution(numbers):
def proof(num):
bnum = bin(num)[2:]
len_bin = len(bin(num)[2:])
next_squ2minus1 = 2 ** (len(bin(len_bin)[2:])) - 1
fill = bnum.zfill(next_squ2minus1)
for idx, val in enumerate(fill, 1):
if idx % 2 == 0 and val == "0":
fir_bin = idx & (-idx)
fir_bin_idx = len(bin(fir_bin)[2:]) - 1
rem_bin = idx & ~(1 << fir_bin_idx)
bef_idx = 0 + rem_bin
aft_idx = (1 << fir_bin_idx+1) - 1 + rem_bin
if any(int(i) for i in fill[bef_idx:aft_idx]):
return 0
return 1
answer = []
for num in numbers:
answer.append(proof(num))
return answer그렇게 완성한 코드다.
정답이라는 직감이 들기는 했는데, 코드가 뭔가 복잡해진 느낌이다.
100점으로 전부 통과하여 정답을 받았다.
하지만, AC 판정을 받고 든 생각이 있다. '내가 오류 확인을 잘못한 건 아닌가?'
왜냐하면 범위를 확인한다고 했는데, 굳이 그럴 필요가 없다는 생각이 자꾸만 들었다.
예를 들어서 8은 1부터 15까지 전 범위를 확인해야 한다.
하지만 실제로 4와 12만 확인하면 되지 않을까?
왜냐하면 4가 2와 6을 확인하고, 2가 1과 3을 확인하고, 6이 5와 7을 확인하고...
이런 식으로 하위 노드에서 어차피 확인을 하기 때문이다.
즉, 처음부터 bef_idx와 aft_idx만 잘못 지정한 걸 내가 너무 어렵게 접근한 건 아닌가하는 생각이 자꾸 들었다.
# -------------------- Before --------------------
fir_bin = idx & (-idx)
fir_bin_idx = len(bin(fir_bin)[2:]) - 1
rem_bin = idx & ~(1 << fir_bin_idx)
bef_idx = 0 + rem_bin
aft_idx = (1 << fir_bin_idx+1) - 1 + rem_bin
if any(int(i) for i in fill[bef_idx:aft_idx]):
return 0
# -------------------- After --------------------
half = (idx & (-idx)) // 2
bef_idx = idx - half - 1
aft_idx = idx + half - 1
if int(fill[bef_idx]) + int(fill[aft_idx]):
return 0그래서 자기 자신의 자식 노드만 확인하는 방법으로 코드를 바꿨다.
2, 4, 8을 봤을 때, 아 부모 노드의 절반만큼 값을 더하고 뺴주면 되는구나 생각했다.
하지만 10, 12, 14 입장에서는 성립하지 않는다.
10과 14는 1만큼 더하거나 빼야 하고, 12는 2만큼 더하거나 빼야 한다.
어라? 위에서 본 코드다. 가장 하위의 1비트 위치만큼 더하거나 빼는 과정이다.
(idx & (-idx))의 절반을 더하거나 뺀다는 말이다.
half에 절반 값을 저장하고, bef_idx와 aft_idx를 계산한다.
bef_idx와 aft_idx에서 1씩 빼주는 이유는 enumerate()의 초기값을 1로 주었기 때문이다.
실제 fill값의 index에 접근하기 위해서는 1을 빼줘야 한다.
그리고 가장 처음에 제출한 코드와 동일하다.
두 값을 더했을 때 True라면 하나라도 1이니 return 0을 한다.
그랬더니 역시는 역시다... 가장 오래 걸린 테스트 케이스가 70ms도 넘지 않는다.
처음 시도해보는 비트마스킹에다가, 2진수와 10진수를 왔다갔다하다보니 헷갈린 점이 많았다.
Refactoring을 조금씩 계속 해주어서 결과적으로 짧은 코드가 완성되기는 했다.
하지만, 처음부터 이런 식으로 깔끔하게 코드를 작성할 수 있게 노력해야 겠다.
조금 더 집중해서 문제 조건을 제대로 파악해야 한다.
이번 문제는 너무 왔다갔다했다는 느낌이 지워지지 않는다. 자꾸 수정할 게 보였다.
그래도 덕분에 비트마스킹과 2진수는 빡세게 공부한 느낌이다.
P.S.1
squ2minus1 = len_bin & (len_bin + 1)작성한 핵심 코드의 이해를 도울 수 있는 코드다.
이 코드를 생각할 수 있으면 작성한 코드들 전부 응용해서 풀 수 있다고 생각한다.
우선 아이디어는 이러하다. '포화 이진트리'라는 것은 2의 N제곱에서 1을 뺀 숫자와 같다.
왜냐하면 포화 이진트리가 되기 위해서는 1개, 2개, 4개, 8개 이런 식으로 루트 노드를 채워야만 한다.
이는 2진수 비트값과 동일하다. 1, 11, 111, 1111. 즉 2의 N제곱에서 1을 뺸 것이다.
num & (num - 1) == 0
비트마스킹을 이용했을 때, 특정 값이 2의 거듭제곱인지 판단하는 식은 위와 같다.
예를 들어 8이 있다고 해보자.
2진수로 하면 1000이고, 1을 뺀 값을 2진수로 바꾸면 111이 된다.
1000과 0111을 AND(&) 연산하면 모든 값이 0으로 바뀐다.
이것을 살짝 응용해서 2의 거듭제곱에서 1을 뺀 숫자를 찾았다.
num & (num + 1) == 0
1을 뺀 값이 아니라, 1을 더한 값을 찾으면 된다.
위에서 2의 거듭제곱 숫자 기준으로, 1을 뺀 숫자와 AND 연산을 하면 0이 된다.
그럼 1을 뺀 숫자 기준으로는 1을 더한 숫자, 즉 2의 거듭제곱과 AND 연산을 하면 0이 된다고 유추할 수 있다.