1. 개요
2. 단순 보안 프로토콜
2.1. 단순 보안 프로토콜
3. 인증 프로토콜
3.1. 인증
3.2. 질문 응답
3.3. 대칭키 상호 인증
3.4. 공개키 상호 인증
3.5. 세션키
3.6. 완전 순방향 비밀성(PFS)
3.7. 타임스탬프
4. TCP 기반 인증
4.1. 3WHS 인증 공격
5. 영지식증명(ZKP)
5.1. 밥의 동굴
5.2. 피아트-샤미르
5.3. 실세계 ZKP
1. 개요
프로토콜은 컴퓨터 내부에서, 또는 컴퓨터 사이에서 데이터의 교환 방식을 정의하는 규칙 체계이다.
쉽게 말하자면, 통신을 위해 상호 약속한 규칙이다.
└ 인간 프로토콜 : 인간 상호 간에 적용하는 규칙
└ 네트워킹 프로토콜 : 네트워크로 연결된 통신 체계에 적용하는 규칙, 예시) HTTP, FTP 등
└ 보안 프로토콜 : 보안 응용에 적용하는 통신 규칙, 예시) SSL, IPSec, 커버로스 등
잘 알려진 보안 프로토콜(IPSec, GSM, WEP 등)에도 결함이 존재한다.
이상적인 프로토콜은 세부 요구사항을 충족해야 한다.
└ 효율성, 견고성, 구현 용이성, 사용 용이성, 융통성 등
모든 요구를 충족하는 프로토콜 설계가 매우 어려운 것이 현실이다.
2. 단순 보안 프로토콜
2.1. 단순 보안 프로토콜
예시 1) NSA 보안 입장 절차
출입증을 판독기에 넣는다 > PIN을 입력한다
if PIN이 유효한가? > 입장 가능
if PIN이 유효하지 않은가? > 총 맞고 사망
예시 2) 현금인출기 프로토콜
현금 카드를 판독기에 넣는다 > PIN을 입력한다
if PIN이 유효한가? > 현금 인출 가능
if PIN이 유효하지 않은가? > 카드 압수

예시 3) 피아식별(IFF; Identify Friend of Foe)
관제탑에서 난 N을 입국하려는 임팔라기에게 전송한다.
이에 임팔라기는 정해진 암호화 규칙에 따라 관제탑에 E(N, K) 값을 전송한다.
관제탑에서는 자신이 가진 E(N, K)값과 비교하여 적군인지 아군인지 판단한다.
임팔라기는 암호화 키 K를 알고 있었기에 아군으로 판단할 수 있다.

예시 4) 중간 미그기
러시아 미그기와 앙골라가 같은 편, 임팔라기와 나미비아가 같은 편이다.
이때 러시아 미그기가 나미비아에 접근하는 것이 목적이다.
러시아 머그기가 나미비아 레이더에 잡혀 난수 N을 받는다.
하지만 머그기는 암호화 키를 모르기에 자신이 받은 N을 앙골라 레이더에게 보낸다.
앙골라 레이더는 자신이 나미비아 레이더인 것마냥 임팔라기에 보낸다.
예시 3의 과정처럼 임팔라기는 앙골라 레이더에게 E(N, K) 값을 보낸다.
앙골라 레이더는 E(N, K) 값을 머그기로 보낸다.
이를 나미비아 레이더로 보내 자신이 임팔라기인 것처럼 속여 접근한다.
3. 인증 프로토콜
3.1. 인증
앨리스와 밥, 두 사람이 서로 통신을 한다고 가정하자.
이때 앨리스와 밥은 서로에게 자신을 인증할 필요가 있다.
이것을 '상호 인증(Mutual Authentication)'이라고 한다.
상호 인증에는 세션키가 필요할 수도 있고, 그외 추가 요구 사항이 있을 수도 있다.
└ 추가 요구사항 : 공개키, 대칭키, 해시 함수, 익명성, 그럴듯한 부인권(Plausible Deniability 등
독립 컴퓨터에서 인증은 상대적으로 용이하다.
하지만 네트워크에서 인증은 훨씬 복잡한 상황이 발생한다.
└ 공격자의 메시지 관찰 가능성, 메시지 수정 및 삽입 삭제 가능성 등

왼쪽은 아주 단순한 독립 컴퓨터 상황에서의 상호 인증을 나타낸 그림이다.
전제 조건으로 밥은 앨리스의 패스워드를 반드시 알아야 한다.
오른쪽은 트루디가 앨리스를 흉내내어 공격하는 '재연 공격' 상황이다.
3.2. 질문 응답

인증 재연을 방지하기 위하여 질문-응답(Challenge-Response)을 사용한다.
밥이 앨리스를 인증하려 할 때, 대답하는 앨리스의 패스워드로 인증한다.
이때 넌스(nonce)를 사용하여 신선도를 유지한다.
└ nonce : 일회 사용 가능한 숫자(number used once)
또한 해시 함수를 이용하여 암호화를 진행한다.
단점은 밥이 앨리스의 패스워드를 알고 있어야 한다.
3.3. 대칭키 상호 인증
앨리스와 밥은 대칭키 Kab를 공유하고, 앨리스와 밥만이 알고 있다.
어떻게 하면 키를 노출하지 않고 재연 공격을 방지하며 구현할 수 있을까?

가장 간단한 형태의 대칭키를 이용한 인증이다.
가장 간단하지만 상호 인증에서는 문제가 있다.
밥이 앨리스를 인증하지만, 앨리스는 밥을 인증하지 않는다.

둘이 가진 대칭키 Kab로 처음부터 인증을 하면 상호 인증이 가능하다.
하지만 이때 송신자가 정말 앨리스인지 확신할 수 있을까?
2번째 메시지와 3번째 메시지는 동일하여 앨리스가 정말 앨리스인지 판단할 수 없다.
오른쪽의 방식으로 진행하면 확실하게 상호 인증을 제공할 수 있다.
하지만 아직도 중간자 공격(Man in the Middle attack)에 약하다.

1. 트루디가 Ra로 밥에게 인증 요청을 한다.
2. 밥은 Rb, E(Ra, Kab)를 트루디에게 송신한다.
3. 트루디는 받은 Rb로 다시 밥에게 인증 요청을 한다.
4. 밥은 Rc, E(Rb, Kab)를 트루디에게 송신한다.
5. 이때 받은 E(Rb, Kab)를 2번에 대한 답으로 인증한다.
이처럼 단방향 인증 프로토콜(non-mutual)은 상호 인증에서 안전성이 보장되지 않는다.

위와 같은 방식으로 변화를 주면 도움이 된다.
3.4. 공개키 상호 인증
앨리스의 공개키로 M을 암호화 : {M}앨리스
앨리스의 개인키로 M을 서명함 : [M]앨리스
이때 [{M}앨리스]앨리스 = M와 {[M]앨리스}M앨리스 = M가 성립한다.

공개키 인증에서 밥은 앨리스를 인증할 수 있다.
트루디가 'C = {M}앨리스'를 가로챘을 때를 가정해보자.
트루디가 C를 앨리스에게 보내면, 앨리스는 복호화된 평문을 트루디에게 보낸다.
전자서명 인증에서는 트루디는 앨리스에게 무엇이든 서명하게 할 수 있다.
때문에 서명과 암호화에 서로 다른 두 개의 키 쌍을 사용해야 한다.
3.5. 세션키

키에 대해서는 안전하나, 상호 인증을 하지 못하는 상황이다.
밥은 앨리스를 인증하였으나, 앨리스는 밥을 인증하지 못한 상태이다.
K가 밥의 nonce 역할을 하고 있다.
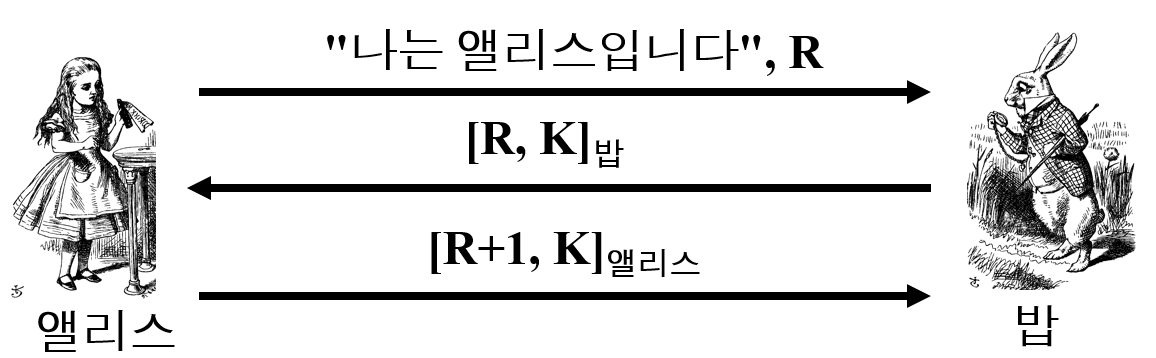
상호 인증을 제공하지만, 누구든지 세션키 K를 알아낼 수 있는 상황이다.

'선 서명 후 암호화'의 상호 인증 및 세션키 인증은 안전한 것으로 판단된다.
'선 암호화 후 서명'의 상호 인증 및 세션키 인증은 안전하나 누구든 값을 관찰할 수 있다.
└ 누구든 {R, K}앨리스 {R+1, K}를 관찰할 수 있다.
선 서명 후 암호화 vs 선 암호화 후 서명
트루디는 K를 복원하기 위해 공개키 암호를 해독해야 한다.
즉, 두 방식에 있어서 보안상의 차이는 없다.
3.6. 완전 순방향 비밀성(PFS)
우려 상황
앨리스는 공유키 Kab로 메시지를 암호화하고 밥에게 전송
트루디는 암호문을 기록해두고, 나중에 Kab를 찾기 위해 앨리스(또는 밥)의 컴퓨터를 공격한다.
트루디는 기록해둔 메시지를 복호화할 수 있다.
완전 순방향 비밀성(PFS; Perfect Forward Secrecy)
트루디가 기록해둔 암호문을 나중에 복호화할 수 없도록 하는 것이다.
PFS를 위해서라면 앨리스와 밥은 Kab를 사용하여 암호화할 수 없다.
대신 세션키 Ks를 사용하고, '망각'해야 한다.
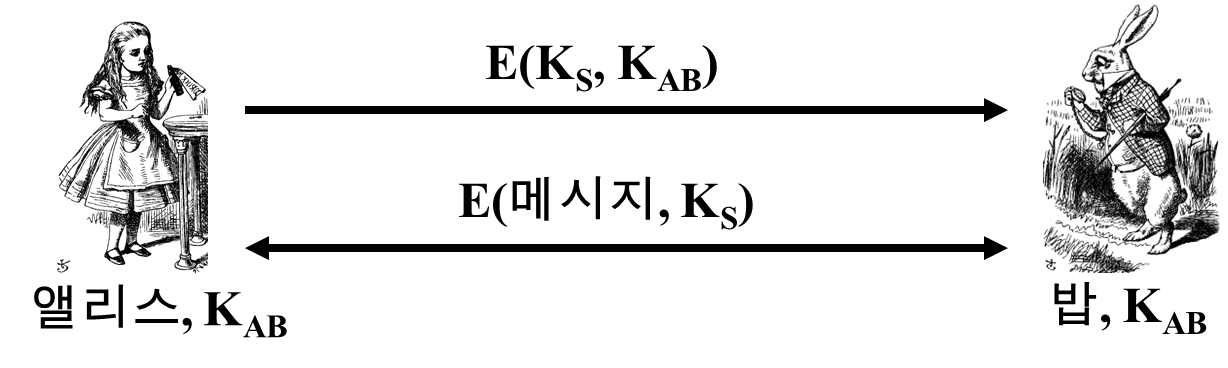
트루디는 E(Ks, Kab)를 기록해둘 수 있다.
트루디가 Kab를 확보하면 자연스럽게 Ks도 확보할 수 있다.

왼쪽의 상황에서 PFS를 위해 디피-헬먼을 이용했다. 이때 g와 P는 공개된 값이다.
디피-헬먼을 단순하게 사용한다면 MiM(Man in the Middle Attack)에 취약하다.
오른쪽의 방식으로 MiM을 방지할 수 있다.
세션키 Ks = gab mod P로 설정한다. 앨리스는 a를 밥은 b를 망각하여 일회성 디피-헬먼을 구현한다.
앨리스와 밥조차도 Ks를 복구하는 것은 불가능하다.
이런 방식으로 PFS를 구현할 수도 있다.

세션키 Ks = gab mod P로 설정한다.
MiM를 방지했던 것처럼 앨리스는 a를 밥은 b를 망각한다.
만약 트루디가 ga와 gb를 얻는다고 하더라도 지수 곱셈에 의하여 ga * gb = g(a+b)가 된다.
결국 트루디는 gab를 구하지 못해 세션키 Ks 복구는 불가능하다.
3.7. 타임스탬프
타임스탬프 T는 현재 시각을 의미한다.
nonce의 경우 양쪽 모두 사전에 알고 있어야 하기에, 타임스탬프는 메시지 개수를 줄여주는 효과가 있다.
타임스탬프 사용은 '시각'이 보안의 주 요소가 된다는 것을 의미한다.
하지만 시간 오차(Clock Skew) 허용은 불가피하다는 점이 있다.

타임스탬프를 이용한 인증 '선 서명 후 암호화'는 안전한 것으로 판단한다.
'선 암호화 후 서명'은 트루디가 '{T, K}밥'을 찾기 위해 앨리스의 공개키를 이용할 수 있다.
└ 서명은 공개키와 개인키가 상호 관계를 갖는다. 즉 앨리스의 개인키로 서명한 값을 공개키로 풀 수 있다.
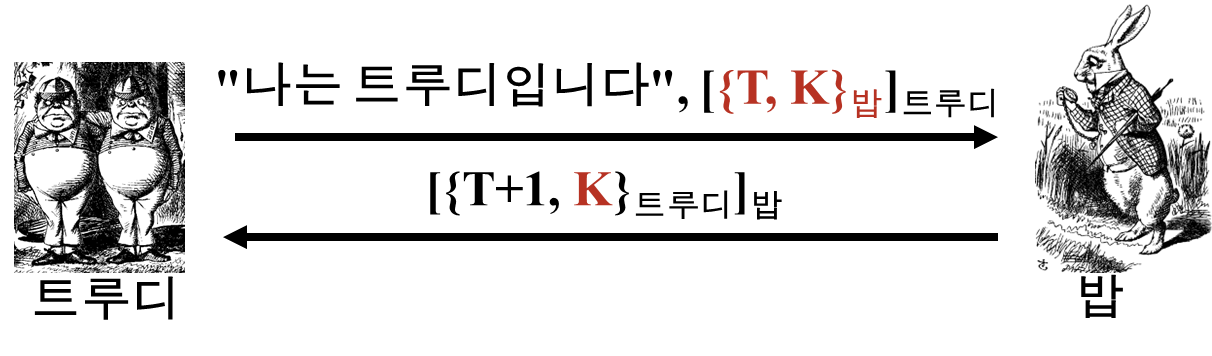
위에서 언급한 것처럼 트루디는 앨리스의 공개키로 '{T, K}밥'을 얻었다.
이를 트루디 자신의 개인키로 서명해 밥에게 보낸다.
밥은 이것이 정상적인 인증 요청이라고 생각해, 서명과 암호화를 해제하고 새로운 응답을 보낸다.
이렇게 트루디는 타임스탬프 T과 세션키 K를 얻을 수 있게 된다.
하지만 트루디는 허용된 시간 오차(Clock Skew) 내에 작업을 수행해야만 의미가 있다.
공개키 인증
넌스와 타임스탬프를 활용한 공개키 인증 방식의 구분이 있다.
ㆍ (nonce 사용) 선 서명 후 암호화 : 안전하다
ㆍ (nonce 사용) 선 암호화 후 서명 : 안전하다
ㆍ (timestamp 사용) 선 서명 후 암호화 : 안전하다
ㆍ (timestamp 사용) 선 암호화 후 서명 : 안전하지 않다
안전하지 않은 timestamp를 사용한 선 암호화 후 서명만을 다룬다.

개선 전 : (밥이 앨리스에게) [{T+1, K}앨리스]밥
개선 후 : (밥이 앨리스에게) [{T+1}앨리스]밥
앨리스는 K를 이미 알고 있고, 밥을 인증하기 위한 목적으로 사용했었다.
밥이 K를 다시 보낼 필요가 없다는 뜻이다.
이럴 때 선 암호화 후 서명은 안전한 것으로 판단된다.
4. TCP 기반 인증
4.1. 3WHS 인증 공격
TCP 프로토콜은 인증 목적으로 설계한 것이 아니다.
하지만 TCP 접속 시 IP 주소를 인증의 수단으로 사용하는 경우가 종종 존재한다.
└ IPsec의 한 모드에서 IP 주소를 인증 목적으로 사용하는 경우가 있다.
이러한 점이 문제를 야기할 수 있다.

TCP 3WHS의 최초 SEQ 번호는 난수여야만 한다.
최초 SEQ 번호가 난수가 아니고 우측처럼 퍼진다면 추측해낼 가능성이 존재한다.

(이때 밥은 웹 서버의 역할을 한다고 가정한다.)
1. 트루디는 자신의 SEQ(t)를 밥에게 보내 3WHS를 시도한다.
2. 밥은 이에 대한 응답(B1)을 보낸다.
3. 트루디는 자신이 앨리스인 마냥 SEQ(a)를 밥에게 보낸다.
└ 송신지 IP를 앨리스의 IP로 속일 수 있다.
4. 밥은 앨리스에게 응답(B2)을 보낸다.
5. B2를 사용하여 결과적으로 트루디와 밥이 3WHS에 성공하게 된다.
└ B1을 기반으로 트루디가 B2를 예측했다고 가정한다.
트루디의 3WHS 성공 후 앨리스는 밥에게 응답을 주지 못하게 DoS 공격을 행한다.
트루디는 밥이 무엇을 전송하는지 알지 못한다.
하지만 자신을 앨리스로 가장하고 서버인 밥과 통신을 해, 인증을 진행할 수 있다.
트루디는 밥이 보내는 패킷을 앨리스가 받지 못하도록 해야 한다.
만약 앨리스가 패킷을 받아 통신을 진행하면 접속이 종료될 것이기 때문이다.
위의 과정 중 패드워드나 다른 인증을 요구한다면 이 공격은 실패한다.
만약 TCP 접속이 인증 그 자체의 수단이 된다면 이 공격은 성공한다.
결론은 TCP로 인증을 수행하는 것은 잘못된, 위험한 거다.
5. 영지식증명(ZKP)
영지식증명(ZKP; Zero Knowledge Proof)은 어떤 것도 노출하지 않고 비밀을 알고 있음을 증명하는 것이다.
이 과정은 확률적으로 결정된다.
└ 밥은 앨리스가 비밀을 알고 있다는 것을 임의의 높은 확률로 확인하면 된다.
이것을 '상호 대화식 증명 시스템'이라고 한다.
5.1. 밥의 동굴

위와 같은 미로가 있다고 가정해보자.
앨리스는 R과 S 사이의 벽을 열 수 있는 비밀 주문을 알고 있다고 주장하고 있다.
앨리스는 비밀 주문을 알려주지 않고도, 자신이 주문을 알고 있음을 어떻게 증명할까?

밥이 Q 위치에 서있고 앨리스보고 S 방향으로 나오라고 한다.
앨리스는 밥이 들을 수 없게 조용히 주문을 외치고 나온다.
앨리스는 주문을 알지 못하는 상태이고, 이미 S에 있을 가능성도 있다.
즉 1/2의 확률로 원하는 방향으로 나올 수 있다.
밥이 N번 반복해서 이런 주문을 한다면, 앨리스가 밥을 속일 확률은 (1/2)^N밖에 안 된다.
5.2. 피아트-샤미르
동굴에 기반한 프로토콜 개념은 불편하다.
이와 같은 개념 없이 ZKP 효과를 달성하는 것을 피아트와 샤미르가 내놓은 이론이다.
p과 q과 소수일 때, N = pq라고 가정해보자.
비밀 정보 : S
공개 정보 : N = S^2 mod N을 충족하는 N, S^2 mod N
이때 앨리스는 비밀 S를 알고 있다.
앨리스는 S에 대한 어떤 정보도 노출하지 않고 S를 알고 있다고 밥에게 증명한다.
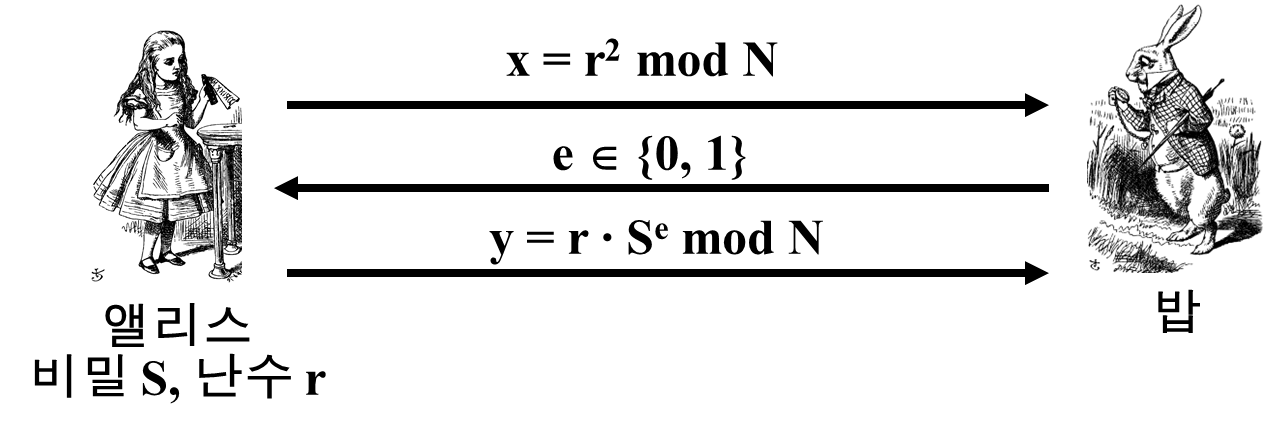
공개 값 : mod N, v = S^2 mod N
앨리스는 비밀 값 S와 난수 r을 가지고 있다.
밥은 임의의 e ∈ {0, 1}를 선택한다.
밥은 y2 = r2 * S2e = r2 * (S2)e = x * ve mod N를 확인한다.

밥이 임의의 e값을 1로 했을 때의 상황이다.
앨리스는 y = r * S mod N을 밥에게 보낸다.
이를 가지고 밥은 y^2 = x * v mod N가 성립하는지 확인해야 한다.
이때 앨리스는 S를 알아야만 위의 식이 성립한다.

밥이 임의의 e값을 0으로 했을 때의 상황이다.
e가 0이기 때문에 밥은 y^2 = x mod N을 확인해야 한다.
y^2 = r^2 = x mod N이다.
이 경우에는 앨리스가 S를 알아야 할 필요가 없다. (어떤 수의 0 제곱은 1이 된다.)
동굴 문제의 1/2 상황을 이렇게 구현했다.
정리
밥은 e ∈ {0, 1}을 선택하여 앨리스에게 질문(Challenge)한다.
앨리스는 y = r * S^e mod N으로 응답(Response)한다.
밥은 y^2 = x * v^e mod N이 성립하는지 확인한다.
과연 이것으로 진짜 앨리스가 응답했음을 증명할 수 있을까?에 대한 의문이 남아있다.
트루디가 밥을 속이려 할 때, 1/2의 확률로 밥을 속일 수 있다.
하지만 위에서 언급했듯 N번일 경우 확률은 (1/2)^N로 기하급수적으로 줄어들게 된다.
또한 앨리스는 매번 다른 난수 r을 사용하여 증명해야 한다.
└ 그렇지 않다면 e가 0일 때 r을 전송하고, e가 1일 때 r * S를 전송하여 결국 S를 찾을 수 있게 된다.
영지식의 비밀 S에 대해 알아내는 것이 전혀 없어야 한다는 것을 의미한다.
ㆍ 공개 값이 v = S^2 mod N일 때
ㆍ 1번 메시지에서 r^2 mod N를 관찰
ㆍ 3번 메시지에서 r * S mod N을 관찰 (e가 1이라면)
만약 밥이 r^2 mod N으로 r을 찾아낼 수 있다면 S를 알아낼 수 있다.
하지만 이는 '모듈러 제곱근 연산'을 요구하는데 RSA 보안 강도와 동일하다.
트루디가 S를 찾아내는데 전혀 도움이 되지 않는다.
결국 이것은 수학적으로 타당하다.
5.3. 실세계 ZKP
공개키로 사용자를 식별할 수 있다.
처음에는 상대방의 공개키를 모르기 때문에 상대의 인증서를 요구한다.
인증서 자체에 식별 정보가 있어, 트루디는 대화 상대를 알 수 있다.
즉, 익명성이 보장되지 않는다는 것이다.
ZKP는 사용자 식별을 하지 않고 인증할 수 있는 한 가지 방법이다.
공개 값 v에는 어떤 식별 정보도 없고, 프로토콜 메시지에도 식별 정보가 없다.
ZKP는 마이크로소프트社의 차세대 보안 컴퓨팅 기반(NGSCB)에 적용했다.
└ NGSCB : Next Generation Secure Computing Base
데이터를 식별하는 장비를 노출하지 않고 소프트웨어를 인증하는데 이용한다.
최상의 기준은 여러 요소에 따라 달라진다.
└ Ex) 시스템 민감도, 지연 시간, 비용, 암호 기법, 세션키 여부, PFS 여부, 익명성 여부 등
정해진 요소에 따라서 실세계에서 적용할 수 있게 개발해야 한다.
'학교 공부 > 스마트 콘텐츠 보안' 카테고리의 다른 글
| 10 실제 보안 프로토콜 (0) | 2023.05.27 |
|---|---|
| 08 인가 (0) | 2023.05.16 |
| 07 인증 (0) | 2023.05.14 |
| 05 해시 함수 (0) | 2023.03.30 |
| 04 공개키 (0) | 2023.03.30 |
