22. NLP Trends - ALBERT
ALBERT - Low Rank Matrix Factorization
ALBERT(A Lite BERT)는 이름 그대로 더 가벼운 버전의 BERT 모델이다.
메모리와 학습 시간이 비대해지는 상황에서, 성능은 올리고 자원은 줄이는 새로운 task를 제안하였다.
해당 task는 Factorized Embedding Parameterization이다.
GPT나 BERT는 Self Attention Block을 계속 쌓으면서 성능을 올리는 모델들이다.
DL 측면에서 Layer를 쌓는 것이 유의미한 정보를 추출하는 과정이기 때문이다.
이때 Input과 Output의 크기는 hidden state vecor와 동일해야 행렬곱 연산이 가능하다.
즉 hidden layer size가 크면 클수록 계산량이 배로 늘어난다.
그렇다고 차원 수를 너무 줄이면 정보를 표현할 수 없는 문제가 있다.
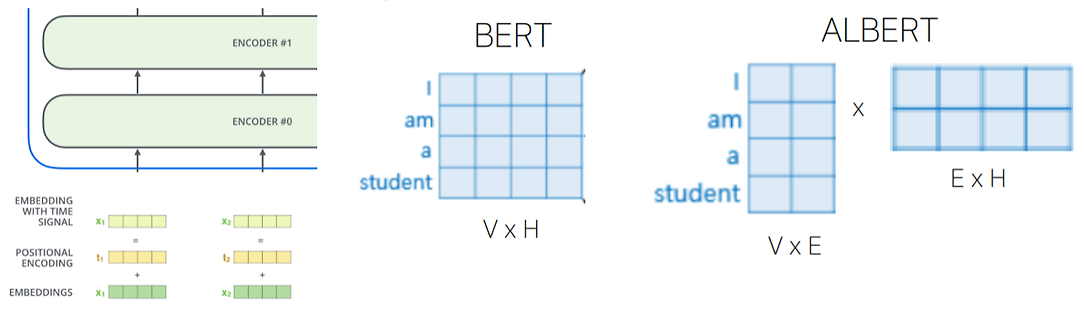
Vocabulary size를 V, Hidden state dimension을 H, Word embedding dimension을 E라고 할 때,
기존 Input size는 V * H만큼의 값을 필요로 한다.
행렬 분해를 통해 V * H를 (V * E) * (E * H)로 쪼갠다면, 필요한 값은 V * E + E * H로 줄어든다.
그럼 굳이 처음 단어들의 embedding을 고차원으로 할 필요가 없다는 말이다.
이를 수학적으로 바라보면 Low Rank Matrix Factorization 혹은 Low Rank Approximation이라고 한다.
간단한 예시로 hidden state dimension이 768이고 단어가 30,000개 있다고 해보자.
그리고 단어별 embedding dimension은 가볍게 128 차원으로 embedding 했다 가정하자.
그럼 원래 계산량은 30,000 * 768로 23M이 나온다.
행렬 분해 후 계산량은 (30,000 * 128) + (128 * 768)로 약 4M에 불과하다.
ALBERT - Cross Layer Parameter Sharing

ALBERT는 input word embedding 외에 parameter 측면에서도 최적화를 시도했다.
Self Attention에서 학습해야 하는 parameter들은 linear transformation에 필요한 가중치 행렬들이다.
더 자세하게 말하면 Multi Head 개수만큼의 가중치 행렬 세트들(W^Q, W^K, W^V)과
출력 dimension을 맞추기 위한 output layer의 linear transformation용 가중치 행렬(W^O)이 여기에 속한다.
만약 한 Block에서 12개의 Head를 사용한다고 하면 12개만큼의 가중치 행렬들이 있는 것이다.
이건 하나의 Self Attention Block에서 이야기이고, Block을 쌓을 수록 배로 늘어난다.

학습할 parameter 수가 너무 많아지니, 이것들을 공유하자는 아이디어에서 출발했다.
ALBERT는 4개로 나누어 parameter sharing을 진행했다.
ㆍ all-shared: 모든 파라미터를 공유하는 방법
ㆍ Shared-attention: attention의 파라미터만 공유하는 방법
ㆍ Shared-FFN: feed-forward network 파라미터만 공유하는 방법
ㆍ not-shared: 모든 파라미터를 공유하지 않는 방법, 기존 BERT 모델이다.
그랬더니 all shared에서 parameter 수는 확연히 줄었지만, 성능은 크게 하락하지 않은 모습을 보였다.
이렇게 여러 개의 Transformer layer가 서로 다른 parameter를 갖지 않고,
하나의 layer 가중치를 반복해서 재사용하는 구조를 Cross Layer Parameter Sharing 방법이라고 한다.
ALBERT - Sentence Order Prediction

Low Rank Matrix Factorization과 Cross Layer Parameter Sharing을 통해 자원을 절약했다.
ALBERT 여기에 이어 SOP라는 방법으로 모델 성능을 향상시켰다.
BERT는 MLM(Masked Language Model)과 NSP(Next Sentence Prediction)를 통해 학습했다.
하지만 후속 연구들에서 NSP는 BERT에서 큰 의미가 없는 방법이라고 자주 거론되었다.
Fine tuning을 하며 MLM로만 학습을 해보니 NSP에는 문제가 있었다.
NSP는 단순 문장 추출(random)을 기반으로 학습했다.
원래 두 문장 중 하나를 아예 다른 문장으로 바꿨기 때문에, 두 문장의 맥락이 너무 다르다든가
연결적 의미가 아니라 표면적 차이로만 비교하기 때문에, 문장 간 의미 관계를 학습하지 못했다.
요약하면, 너무 쉬웠다는 말이다.
그래서 보다 어려운 구조적 관계를 학습하기 위해 SOP라는 방법을 고안했다.
SOP(Sentence Order Prediction)는 연속한 문장의 순서를 바꿔, 이 순서가 맞는지 틀린지 판단하는 task다.
두 문장의 순서가 올바르다면 YES, 아니라 순서가 바뀌었다면 NO를 뱉는다.
따라서 NSP에 비해 문장의 흐름을 파악해야지만 맞출 수 있는 문제로 바뀐 것이다.

위 표는 ALBERT 논문에서 None(only MLM), NSP, SOP의 성능을 비교한 표다.
None과 NSP는 실제로 큰 차이가 없고, 때때로 None이 더 점수가 높은 경우도 있다.
SOP를 pretraining task로 적용한 경우, 대부분의 NLP에서 성능이 높아짐을 확인할 수 있다.

위는 GLUE 데이터 셋에 대한 ALBERT 모델의 벤치마크 결과다.
전반적으로 모델은 가벼워졌지만, 성능은 향상한 것을확인 할 수 있다.
P.S.
ALBERT의 input parameter 경량화 부분에서 행렬을 쪼개는 방식을 설명할 때
Low Rank Matirx Factorization 혹은 Low Rank Approximation이라고 언급했다.
하지만 사실 이 두 가지 개념은 동일하지 않고, 다른 개념이다.
ALBERT는 Low Rank Matrix Factorization이 맞는 말이다.
Low Rank Maxtirx Factorization은 용어 그대로 정확히 행렬을 분해해야 한다.
주어진 행렬을 낮은 차원 행렬들의 곱으로 정확하게 표현할 수 있어야 한다.
대게 모델 학습에서 자원을 줄이거나, 새로운 의미를 찾기 위해 자주 사용한다.
이에 비해 Low Rank Approximation은 용어 그대로 근사값이면 괜찮다.
주어진 행렬을 가장 비슷한 낮은 차원 행렬로 근사하는 것이다.
차원을 축소하거나 압축해야 할 때 사용한다.
표로 비교하자면 다음과 같다.
| Low Rank Matrix Factorization | Low Rank Approximation | |
| 정의 | 주어진 행렬을 낮은 rank 행렬들의 곱으로 정확하게 분해 |
원래 행렬을 가장 비슷한 낮은 rank 행렬로 근사 |
| 목적 | 구조적 표현 (잠재 변수 찾기, 모델 학습) |
정보 압축, 근사, 차원 축소 |
| 정확성 | 손실 없이 정확하게 맞춤 | 정확하지 않아도 되는 근사 |
| 예시 | BERT의 factorization, 추천 시스템의 MF |
SVD truncation, PCA, LSA |
| 수학 표현 | A = UㆍV^T | A ≒ U_k Σ_k V^T_k |