17. Transformer - Positional Encoding
Positional Encoding
Attention이라는 계산 방법 특성상 위치 정보는 representation vector에 포함하지 않는다.
예를 들어 [Stars, shine, bright]라는 입력이 있을 때 이 순서대로 Attention을 수행하는 것과
[bright, shine, Stars]라고 입력을 뒤집어서 Attention을 수행하는 것은 동일하다.
왜냐하면 입력 단어 Q와 문장 전체 (K, V)의 값 자체를 Linear Transformation하고 Weighted Sum하기 때문이다.
쉽게 말하면 곱셈과 덧셈은 순서가 바뀌어도 결과가 같다는 말이다.
Attention의 이러한 점을 보안하기 위해, 위치 정보 vector를 더해서 encoding을 진행한다.
가령 [Eyes, speak, truth]라는 입력의 초기 embedding을 [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]라고 해보자.
그럼 Q로 사용할 단어 위치에 1000을 더해주는 것이다.
Eyes는 첫 번째 단어이기에 [1001, 2, 3]으로 바뀌고, speak는 두 번째 단어라 [4, 1005, 6]으로 바뀌는 식이다.
만약 [truth, speak, Eyes]라는 입력에서는 Eyes는 [1, 2, 1003]이라는 다른 vector를 가지게 된다.
이런 식으로 순서를 구분할 수 있는 unique한 상수 vector를 더하는 것을 Positional Encoding이라고 부른다.

당연하게도 위치 정보에 단순 1000을 더하는 방식은 사용하지 않는다.
위치 정보를 더해주기 위해서는 지켜야 할 두 가지 규칙이 있다.
1. 모든 위치 정보는 sequence나 Input에 관계없이 고유하면서 동일한 식별자를 가진다.
그래야 모델이 위치 자체의 패턴을 학습할 수 있기 때문이다.
즉 sequence가 바뀌더라도 위치 embedding은 동일하게 유지해야만 한다.
이런 이유 때문에 0부터 1까지 값을 Normalization 하는 방식의 embedding도 불가능하다.
Sequence 길이에 따라 같은 위치여도 위치 vector가 달리지기 때문이다.

2. 모든 위치 정보는 너무 크면 안 된다.
위칫값이 너무 커져버리면 단어 간의 상관관계나 유추할 수있는 정보를 왜곡할 수 있게 된다.
이 경우 Attention 과정에서 제대로 학습이 안 될 수 있기 때문이다.
이런 이유 때문에 n번째 token에 [n] * (token index)처럼 정숫값을 부여할 수도 없다.

때문에 Sine 함수와 Cosine 함수를 사용한다.
두 함수는 주기 함수이기 때문에 특정 position마다 일정한 값을 가지게 된다.
또한 -1에서 1 사이를 반복하는 주기 함수이기 때문에 값이 너무 커지지 않는다.
이때 Sigmoid나 tanh처럼 특정 구간의 값으로 변환하는 함수를 사용해도 되지 않나? 의문이 들 수 있다.
활성화 함수는 주기 함수가 아니기에 sequence 길이가 길어지면, 위에서 말한 Normalization의 문제가 발생한다.
더욱이 위치 vector의 차이가 미미하기에 학습에 문제가 있을 수 있다.
여기서 한 가지 의문이 더 들 수 있다.
위치 vector는 고유해야 하는데 주기 함수라면 같은 값이 생길 수도 있지 않는가?에 대함이다.
놓치지 말아야 할 점은 positional encoding은 scalar가 아니라 vector라는 점이다.
그것도 단어와 같은 차원을 가지는 vector라는 것이다.
따라서 서로 다른 주기(혹은 frequency)를 갖는 Sine 함수와 Cosine 함수를 번갈아가며 쌓으면 해결할 수 있다.

위 그림은 positional encoding을 위해 sine & cosine 함수를 그린 차원의 일부 시각화다.
수많은 차원 중 4부터 7까지 차원만을 발췌하였고, 서로 다른 주기(혹은 frequency)를 가짐을 볼 수 있다.
또한 4차원 6차원은 sine 함수 5차원 7차원은 cosine 함수로, 번갈아 사용하는 것도 볼 수 있다.
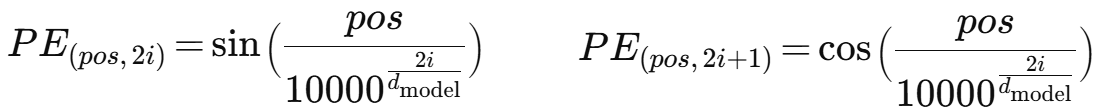
이를 수식으로 나타내면 위와 같다.
pos는 문장에서 단어의 위치, i는 차원 인덱스, d_model은 embedding 차원 수를 의미한다.
상수 10000은 주기 다양성을 확보하고 성능이 뛰어나도록 논문 저자들이 실험을 통해 선택한 값이다.
└ 지수 분포 형태라서 차원마다 log scale 주기 간격을 갖게 된다.
해당 상수를 바꿔도 되지만 작아지면 주파수 간 간격이 좁아지고, 커지면 너무 느려서 표현력이 떨어질 수 있다.
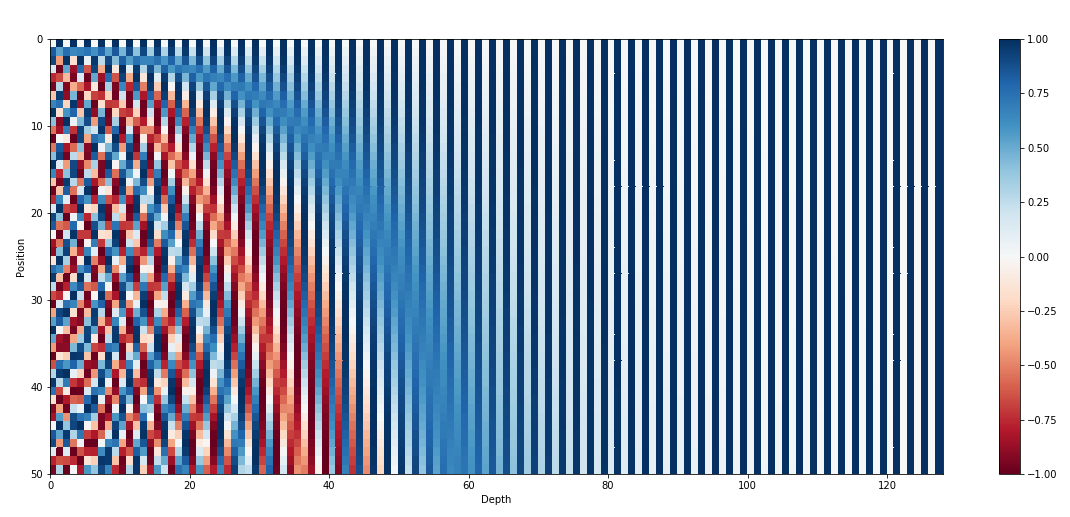
Positional Encoding 결과를 heatmap으로 시각화한 예시는 위와 같다.
Warm up Learning Rate Scheduler

Gradient Descent나 이보다 발전형인 Adam 등의 과정에서 모두 Learning Rate는 하나의 상숫값이다.
하지만 다른 학습 속도를 높이고, 최종 모델의 성능을 올리기 위해 Learning Rate도 학습 중에 적절히 변경하도록 한다.
이를 Learning Rate Scheduler라고 부른다.
Transformer는 처음 학습할 때 가중치가 불안정하게 초기화된 상태다.
이때 너무 큰 learning rate로 시작하면 발산하거나 수렴에 실패한다(왼쪽 그래프의 Large learning rate 상황).
그래서 처음 일정 step 동안은 learning rate를 점진적으로 증가시킨다.
이 과정을 Warm up 단계라고 부른다.
오른쪽 그래프에서 x축(iter)에 따라서 peak까지 올라가는 부분에 해당한다.
이후 특정 iter(혹은 epoch)까지 도달하거나, 어느 정도 학습을 진행한 후에는 다시 학습률을 줄인다.
계속해서 learning rate를 늘리거나 고정값으로 학습을 진행한다면, 좋은 영역에 더 들어가지 못하게 된다.
따라서 큰 보폭 대신 미세 조정하는 부분이 필요하다.
이 과정을 learning rate decay라고 부른다.
이때 얼마나 어떻게 learning rate를 줄일지에 대해서도 많은 방법이 있다.

이를 수식으로 나타내면 위와 같다.
d_model은 embedding 차원 수, step은 현재 학습 단계, warmup_steps는 워밍업 단계 수를 의미한다.
High Level View

Transformer의 전체 구조에 대해서 잠시 짚고 넘어가보자.
입력을 받고 이를 embedding한다. 그 후 Positional Encoding하여 위치 정보를 추가한다.
위치 정보까지 추가한 vector를 Q, K, V로 나누어 Multi Head Attention을 수행한다.
Residual Connection과 Normalization으로 안정화하고 성능을 높인다.
Feed Forward Network를 거친 뒤, 한 번 더 안정화를 진행한다.
이 전체 과정을 Block이라고 부르며, 해당 Block의 N번 쌓아 반복한다.
n번 Block의 결과를 n + 1번 Block의 결과로 넣어주고, 최종 N번 Block의 결과를 Decoder의 입력으로 준다.

Encoder에서 특정 Layer의 Self Attention 패턴을 시각화한 자료다.
위에 있는 단어들이 Query일 때, 아래에 있는 입력 vector에서 어떤 정보를 가져가는지 패턴화했다.
단어 making이 Query로 들어갔을 때, 2009, making, more, difficult 같은 단어들과 주요 관계가 있다.
difficult를 보면 여러 색상을 가지는 greed가 존재하는데, 이는 각각 i번째 Head의 Attention을 의미한다.
각 row마다 하나의 Head라는 뜻이다.
분홍색 Head를 보면 2009, making 등의 시간 정보를 취하는 Head로 보이고,
보라색 Head를 보면 making, <EOS> 등의 자기 자신의 정보를 취하는 Head도 보인다.
Colab 코드에서 다른 시각화 패턴 예시들을 확인할 수 있다.