그래프(Graph)
1. 개념

그래프(Graph)는 원소 사이의 다대다 관계를 표현하는 자료 구조이다.
버스 노선도, 전철 노선도, 인간 관계도, 수도 배관 시스템, 물질의 분자 구조 등 다양한 관계를 표현할 수 있다.
위와 같은 예시들은 선형 자료 구조나 트리 자료 구조로는 표현할 수 없다.
그래프는 연결할 객체를 나타내는 정점(Vertex)과 객체를 연결하는 간선(Edge)의 집합으로 정의한다.
어떤 그래프가 있을 때, 얘는 항상 정확하게 이거!라고 부르기보다는, 조합에 가깝다고 생각한다.
그래프를 어떤 분류로 나누냐에 따라 다양하게 정의할 수 있기 때문이다.
따라서, 해당 글에서는 분류에 초점을 맞추어 살펴보려고 한다.
또한, 트리(tree)도 그래프의 일종이지만, 트리 하나로도 종류가 다양하기에 추후 자세히 살펴본다.
2. 용어 설명
차수(Degree) : 정점에 부속되어 있는 간선의 수
진입 차수(In-Degree) : 정점을 머리로 하는 간선의 수
진출 차수(Out-Degree) : 정점을 꼬리로 하는 간선의 수
경로(Path) : 기점부터 종점까지 간선으로 연결된 정점을 순서대로 나열한 리스트
경로 길이(Path length) : 경로를 구성하는 간선 수
단순 경로(Simple Tree) : 모두 다른 정점으로 구성된 경로
사이클(Cycle) : 단순 경로 중 기점과 종점이 같은 경
DAG(Directed Acyclic Graph) : 방향 그래프이면서 사이클이 없는 그래프, 트리도 DAG의 일종
3. 방향성에 따른 분류

무방향 그래프(Undirected Graph) : 간선에 방향이 없는 그래프
방향 그래프(Directed Graph) : 간선에 방향이 있는 그래프
4. 연결성에 따른 분류

연결 그래프(Connected Graph) : 모든 정점 쌍 사이에 경로가 있는 그래프
비연결 그래프(Disconnected Graph) : 일부 정점 쌍 사이에 경로가 없는 그래프
5. 순환성에 따른 분류

순환 그래프(Cyclic Graph) : 하나 이상의 순환을 포함하는 그래프
비순환 그래프(Acyclic Graph) : 순환을 포함하지 않는 그래프
6. 특별한 속성에 따른 분류

가중치 그래프(Weighted Graph) : 간선에 가중치가 있는 그래프
이분 그래프(Bipartite Graph) : 정점을 두 개의 그룹으로 나눌 수 있는 그래프
완전 그래프(Complete Graph) : 모든 정점 쌍이 서로 연결된 그래프

다중 그래프(Multigraph) : 두 정점 사이에 여러 간선이 있는 그래프
단순 그래프(Simple Graph) : 두 정점 사이에 최대 하나의 간선만 있는 그래프
정규 그래프(Regular Graph) : 모든 정점의 차수가 동일한 그래프
7. 트리와 숲
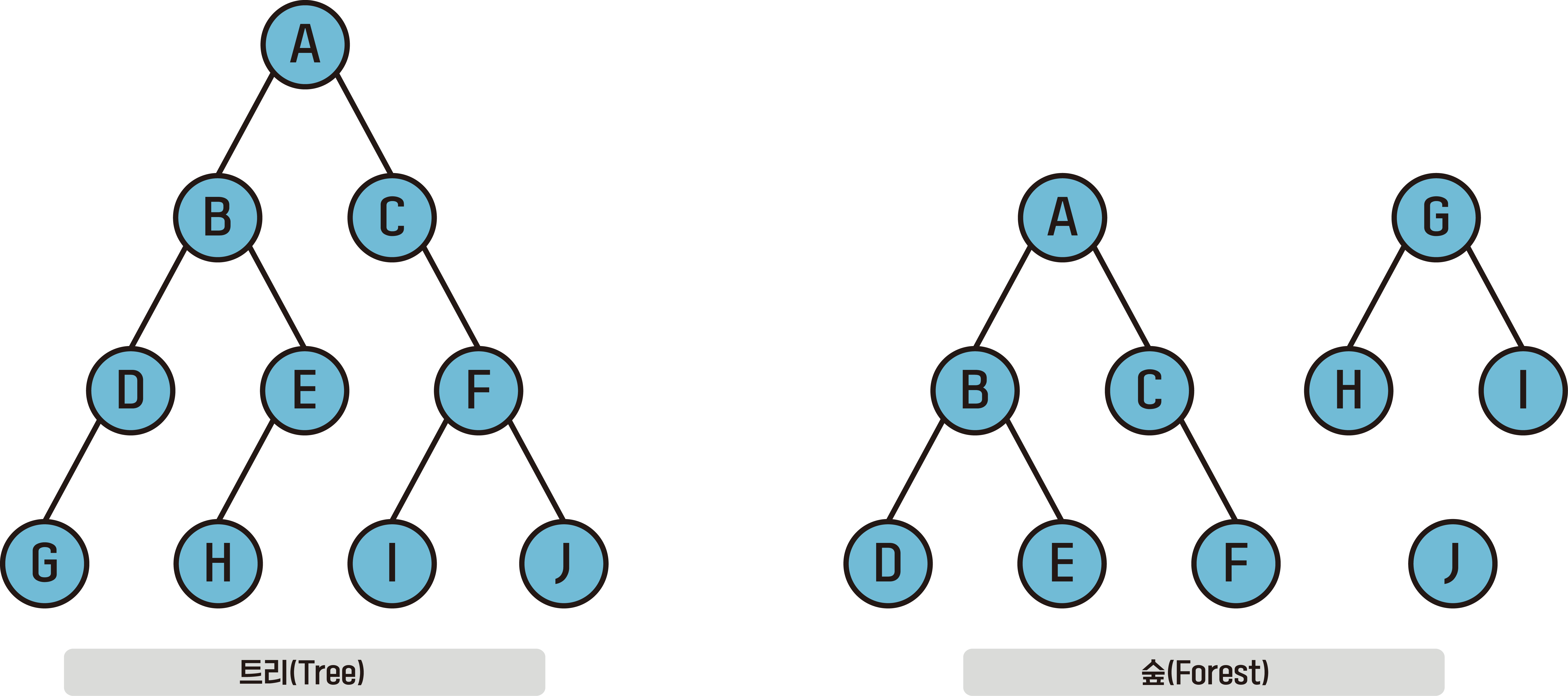
트리(Tree) : 연결되어 있으며 순환 없는 비순환 그래프
숲(Forest) : 하나 이상의 트리로 이루어진 비순환 그래프
8. 응용

위와 같은 그래프는 어떤 그래프일까? 보는 방법에 따라서 달라질 수 있다.
방향성 기준에서 본다면, 무방향 그래프이다.
연결성 기준에서 본다면, 연결 그래프이다.
순환성 기준에서 본다면, 순환 그래프이다.
동시에 최대 하나의 간선만 가지므로 단순 그래프이면서,
모든 정점의 차수가 같아 정규 그래프이기도 하다.

이 그래프는 방향 그래프면서 비연결 그래프고, 비순환 그래프면서 단순 그래프다.
동시에 AC, DBE는 각각 트리이면서, 전체적으로 보면 숲을 이룬다.

조금 특이한 정점이 하나 뿐인 이것은 그래프라고 부를 수 있을까?
처음에 그래프는 '정점과 간선의 집합'이라고 정의했다.
정점이 1개, 간선은 0개인 집합이다. 따라서 하나 뿐인 정점도 그래프가 맞다.
공집합도 집합이지 않은가?
간선이 없기 때문에 방향, 무방향 판별은 무의미하다.
그렇지만 비연결 그래프이고, 비순환 그래프면서
간선이 0개이기에 '최대 하나의 간선'을 가져야 하는 단순 그래프도 만족한다.
또한, 모든 정점의 차수가 0인 정규 그래프도 마찬가지로 만족한다.
무엇보다 이분 그래프도 될 수 있다.
9. 결론
백준이라는 알고리즘 트레이닝 사이트에서 열심히 문제를 풀어보고 있다.
그러다보니 어느덧 단계별로 풀어보기는 31단계까지 왔다.
그렇게 '31단계 그래프와 순회'의 마지막 문제를 풀다가 의문이 들었다.
'내가 그래프의 개념을 잘못 알고 있었나?'
그래프를 '사이클이 존재하는 간선과 정점의 모임'으로 알고 있었다.
문제를 해석하다가 '모든 정점이 다 이어진 입력만 주어지나?'
'어라? 그래프가 입력으로 주어진다고 했는데, 정점이 끊어진 것도 그래프가 될 수 있나?'
하는 의문에 휩싸였고... 전공책을 다시 꺼내들었다.
그리고 놀랍게도 개념을 잘못 알고 있었다는 사실을 깨달았다.
문제를 풀수록 '정확한 개념'을 바탕으로, '유연한 사고'를 생각하는 게 중요하다.
특히 그래프 같은 경우, 어떻게 바라보는냐에 따라서 달라질 수 있다.
이를 바탕으로, 비연결(단절)인 경우, 정점이 하나인 경우 등 다양하게 고려해야 한다.
문제를 다양하게 바라보고 해석할 줄 알아야 한다.