[백준] No.1067 이동 01

열흘이다.

더도 말고 덜도 말고 딱 열흘.

이 문제를 풀기 위해, 아무것도 모르는 상태에서 온갖 영상과 자료를 뒤져가면서 하루종일 몰두한 시간이다.

진짜 대학을 다니면서 4.5로 과탑을 했을 때보다 훨씬 행복하다.

기쁨에 사무쳐 여운이 가시지 않는다.

입에서 '와'라는 탄성만이 연이어 나를 사로잡는다.

내가 해냈다.

 

위 그림은 인랩의 매크로 탐지 그래프 과정 중 일부분이다.

유저의 키보드 신호와 행동 패턴을 하나의 시간 요소로 보고, 주파수 측면으로 변형하는 것이다.

그럼 위처럼 일반 유저와 어뷰저의 행동 패턴이 두드러지게 바뀌는 것을 볼 수 있다.

이 변환에 사용하는 것이 바로 '푸리에 변환'이다.

 

이것은 내가 정말 좋아하는 영상 중 하나이다.

Veritasium이라는 유튜브의 영상으로, 아날로그 적분에 대한 영상이 담겨있다.

더욱이 아날로그 컴퓨터란 무엇인지, 이것이 어떤 변천을 거쳤는지도 가볍게 알 수 있다.

아날로그 컴퓨터의 기원이 되는 이 파동분석기는 William Thomson이라는 사람이 고안했다.

현재는 Kelvin이라는 이름으로 잘 알려져 있으며, 절대온도의 그 '캘빈'이 맞다.

 

내용 중에서 여운이 남았던 것은, 수학과 파동분석기를 이용한다면 조수(파도)를 예측할 수 있다는 것이다.

바로 이 과정에 사용하는 것이 바로 '푸리에 변환'이다.

조수 예측을 아주 제대로 사용한 것이 '제 2차 세계대전'이다.

연합군이 재빠른 침공을 위해 조수를 예측하여, 언제가 가장 유리한지 파악하게 해주었다.

제 2차 세계 대전을 하니 생각나는 이야기가 하나 더 있다.

 

제 2차 세계대전에서 미국은 나가사키와 히로시마에 원자폭탄을 투하했다.

이로 인해 전세계 사람들은 에너지의 위험성을 알게 되었다.

물론 그것은 방대한 에너지 때문만은 아닐 것이다. 강력한 방사능을 포함하고 있으니 문제가 되는 것이다.

그래서 각국에서 핵 연료에 대한 모든 활동을 금지하는 조항을 체결하기로 했다.

하지만 당시 소련은, 미국의 핵 군사력 강화를 위한 책략이라 여겼고, 곧 의미가 퇴색했다.

 

타국에서 핵을 연구하는지 아닌지 감시해야만 하는 상황에 닥쳤다.

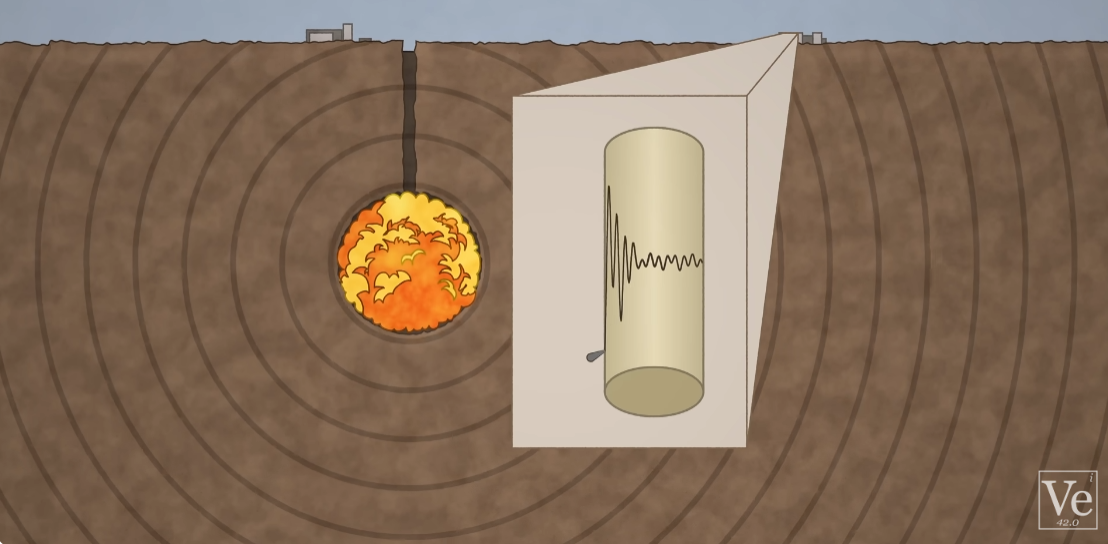
방사성 동위원소가 대기 중에서는 수 천km를 날아가기 때문에 감지가 쉽다.

해저에서도 특수한 소리를 잡는 청음기로 포착이 쉽다.

하지만 지하라면 이야기가 달라진다. 방사성 동위원소도 소리도 널리 퍼지지 않는다.

오직 진동만이 전달되는데, 이를 잡기 위해 사용한 것이 '푸리에 변환'이다.

그리고 이 계산을 빠르게 하기 위해서 '고속 푸리에 변환'이 나온 것이다.

빠르게 적국의 핵 실험을 포착해야 하기에 당연한 이유이다.

(참고로 위 영상도 Veritasium의 유튜브이다.)

 

필요가 있어야 배움이 잘 된다.

FFT를 알기 위해서는 DFT를 알아야 한다.

DFT를 알기 위해서는 FT를 알아야 하고, Convolution을 알아야 한다.

하나하나 근원을 따라가며 차근차근 이해를 하면서 거슬러 올라왔다.

위 내용을 전부 이해했더라도, 코드로 옮기는 과정은 또 다른 일이었다.

 

그래도 많은 참고 자료를 확인하면서 AC를 뚫는 쾌거를 이뤘다.

위에서 설명한 수학 개념들과 유도 과정들은, 참고 자료와 함께 글로 작성할 예정이다.

여기서는 간단(?)하게 어떤 식으로 접근했는지 설명을 한다.

최대한 일관성있게, 일반적이게, 직관적으로 보이도록 노력했다.

 

1067번: 이동

티어가 높을수록 문제 자체는 쉬워지는 느낌이다. 

하지만 그 안에 숨어있는 묘리를 파헤쳐야 한달까...

X와 Y가 있을 때, 둘 다 순환 이동(queue의 rotate 연산)이 가능하다.

X와 Y의 요소를 각각 곱하고 더하는 연산을 한다고 했을 때, 가능한 최댓값을 묻는 문제이다.

 

정말 간단하게 생각한다면, O(N^2)으로 풀 수 있다.

문제에서 요구하는 연산을 수행하고, 최댓값과 비교하고, 순환 이동을 한다. 이걸 반복한다. 

이 순환 이동에 유의해야 한다. 푸리에 변환의 연산곱에 대한 힌트다.

 

from cmath import exp, pi
import sys
input = sys.stdin.readline

우선 호출 부분이다.

기본적으로 빠른 입력을 받는 sys, stdin.readlin을 사용했다.

cmath의 exp(자연 상수 e)와 pi(원주율 𝝿)를 호출한다.

이때 math와 cmath의 차이점은 실수와 복소수의 차이다.

math, cmath 모두 exp, pi를 지원하지만, 푸리에 변환은 복소수 개념에서 동작한다.

따라서 from math import exp, pi가 아닌, from cmath import exp, pi를 해야 한다.

 

length = int(input())
N = 1 << length.bit_length() + 1

X = list(map(int, input().split())) * 2   + [0] * (N - length * 2)
Y = list(map(int, input().split()))[::-1] + [0] * (N - length)

X_FFT = FFT(X, 1)       # FFT
Y_FFT = FFT(Y, 1)       # FFT
mul = [X_FFT[i] * Y_FFT[i] for i in range(N)]

inverse = FFT(mul, -1)  # IFFT
print(max(round(real_num.real / N) for real_num in inverse))

전체적인 Main 코드의 흐름을 짚어보자.

리스트의 길이를 입력받고, 아무튼 무슨 연산을 해서 N을 설정한다.

설정한 N을 이용해서 X와 Y 리스트를 입력받아서 아무튼 무슨 연산을 수행한다.

그리고 각각 FFT(고속 푸리에 변환)을 한다.

X_FFT와 Y_FFT를 각각 곱한 뒤, IFFT(역 고속 푸리에 변환)을 한다.

이 값들 중 가장 큰 값을 찾아내면 정답이다.

 

length = int(input())
N = 1 << length.bit_length() + 1

bit_length() 내장 함수는, 숫자가 몇 자리 bit를 갖는지 반환하는 함수다.

입력받은 length의 bit를 세고, 이것보다 한 자리 더 크게 shift 연산을 하여 N에 저장한다.

그렇다면 N은 무슨 의미일까.

 

예를 들어 length가 3이라고 가정해보자.

그럼 3은 2진수로 11이기에, length.bit_length()를 하면 2가 나온다.

만약 1 << length.bit_length()를 하면 1을 왼쪽shift를 2칸하여 100이 된다.

즉, 1 << length.bit_length()는 현재 숫자에서 (큰 쪽으로) 가장 가까운 2의 제곱수가 된다.

 

그럼 length.bit_length()보다 1 크게 shift하면?

현재 숫자에서 (큰 쪽으로) 2번째로 가까운 2의 제곱수가 된다.

3이라면, 3보다 큰 2의 제곱수들이 4, 8, 16, 32, ... 있으니 2번째인 8을 나타낸다.

15라면, 15보다 큰 2의 제곱수들이 16, 32, 64, 128, ... 있으니 2번째인 32를 나타낸다.

 

이렇게 구하는 이유는 바로 밑에서 알 수 있다.

 

X = list(map(int, input().split())) * 2   + [0] * (N - length * 2)
Y = list(map(int, input().split()))[::-1] + [0] * (N - length)

기본적으로 이 문제를 해결하는 아이디어는 이렇다.

X와 Y 중 하나를 뒤집고, 나머지 하나는 2배만큼 만들어준다.

(푸리에 변환(fourier transform)의 기본인 합성곱(convolution) 연산을 안다는 전제 하에 설명한다.)

예를 들어서 X가 [1, 2, 3, 4]이고 Y가 [5, 6, 7, 8]이라고 가정해보자.

그럼 X는 [1, 2, 3, 4, 1, 2, 3, 4]로 두고, Y는 [8, 7, 6, 5, 0, 0, 0, 0]으로 둔다.

이 상태로 convolution하는 것이다!

그렇게 나온 값들 중 최댓값이 그럼 정답이 된다.

 

FFT의 기본 동작은 divide and conquer(분할 정복)이다.

그 중에서도 리스트의 길이가 2의 제곱일 때만 분할 정복이 가능하다.

(정확하게는 2의 제곱이 아니어도 불가능한 건 아니지만, 과정이 복잡해진다.)

그래서 처음에 0을 패딩해주기 위해서, N을 2의 제곱수로 구한 것이다.

 

예를 들어서 length가 3이었다면, 3 * 2 = 6으로, 가장 첫 2의 제곱수는 4로 자리가 부족하다.

그래서 2번째로 가까운 2의 제곱수를 구해준 것이다.

 

X 리스트를 입력받고, 2배로 만든다. 그리고 남은 자리를 0으로 패딩한다.

Y 리스트를 입력받고, 뒤집는다. 그리고 남은 자리를 0으로 패딩한다.

예를 들어서 X가 [1, 2, 3]이고, Y가 [5, 6, 7]이라고 가정해보자.

그럼 X는 [1, 2, 3, 1, 2, 3, 0, 0]이고, Y는 [7, 6, 5, 0, 0, 0, 0, 0]가 된다.

물론 length가 2의 제곱수라면 의미없는 0이 뒤에 붙을 수 있다.

하지만 0이기 때문에 convolution 연산의 결과는 0으로 무시가 가능하다.

 

X_FFT = FFT(X, 1)       # FFT
Y_FFT = FFT(Y, 1)       # FFT

mul = [X_FFT[l] * Y_FFT[l] for l in range(N)]
inverse = FFT(mul, -1)  # IFFT

X와 Y를 각각 FFT 연산을 하여 저장한다.

그리고 두 요소를 각각 곱해서 mul이라는 리스트에 따로 저장해준다.

mul 리스트를 IFFT(역 연산)를 수행하면, 원하는 결괏값들이 나온다!

 

print(max(round(real_num.real / N) for real_num in inverse))

역 연산을 수행해서 나온 inverse 리스트는 현재 복소수가 들어가 있다.

이렇게 정규화하는 이유는 FFT 과정 중에 각 요소가 N만큼 곱해졌기 때문이다.

이를 전체 길이 N으로 나누어 정규화해야 한다.

 

또한, 여기서 원하는 값은 정수다. 즉 변환을 해줘야 한다.

real 메소드를 사용하면, a + bi의 복소수 형태에서 실수만을 취해준다.

복소수만큼 손실이 발생했기 때문에, round() 함수로 반올림 해준다.

그리고? 이들 중 최댓값(max)를 구하면 된다.

 

def FFT(a: list, inverse: int) -> list:
    N = len(a)
    if N == 1: return a
    
    even = FFT(a[0::2], inverse)
    odd  = FFT(a[1::2], inverse)

    w_N = [exp(inverse*2j*pi*n/N) for n in range(N//2)]
        
    frt = [even[i] + w_N[i] * odd[i] for i in range(N//2)]
    bck = [even[i] - w_N[i] * odd[i] for i in range(N//2)]
    return frt + bck

대망의 FFT 알고리즘이다.

수학자 두 명이 고안해낸 '쿨리-튜키 알고리즘(Cooley-Tukey algorithm)'을 따라간다.

더 넓은 범위, 더 빠른 속도를 원한다면 'NTT(Number Theoretic Transform)'라는 알고리즘을 사용하기도 한다.

정수론의 소수(MOD)와 원시근을 이용한 방법이다. 하지만 여기서는 사용하지 않는다.

 

쉽게 말하면 DFT(이산 푸리에 변환)에서 중복으로 발생하는 연산이 있다.

중복은 주어진 전체 길이를 반으로 쪼갰을 때를 기준으로 존재한다.

따라서 반으로 나눠서 다시 푸리에 변환을 진행하는 방식으로 수행한다.

 

def FFT(a: list, inverse: int) -> list:

리스트 a와 정수 inverse를 입력받는다.

a는 FFT할 리스트이고, 정변환인지 역변환인지 나타내는 inverse 변수다.

놀랍게도 FFT와 IFFT는 단 하나의 값만 다르다!

따라서 코드를 아주 손쉽게 재사용할 수 있다.

 

N = len(a)
if N == 1: return a

 

리스트 a의 길이는 추후에도 사용하기에 N에 저장해준다.

N이 1이라면 더 이상 쪼갤 수 없다. 이때는 a를 그대로 반환하면 된다.

 

even = FFT(a[0::2], inverse)
odd  = FFT(a[1::2], inverse)

위에서 푸리에 변환을 나눈다고 언급했다.

기함수와 우함수의 특징을 이용하여, 홀수 번째와 짝수 번째 index를 기준으로 나눈다. 

(기함수는, 다른 말로 홀함수이다. y(-x) = -y(x)가 성립하는 특징을 갖는다.)

(우함수는, 다른 말로 짝함수이다. y(x) = y(-x)가 성립하는 특징을 갖는다.)

나눈 리스트는 FFT로 재귀를 돌려준다.

 

w_N = [exp(inverse*2j*pi*n/N) for n in range(N//2)]

나중에 곱해주기 위해서 가중치를 미리 리스트로 만들어둔다.

푸리에 변환에 의해 가중치 e^2𝝿jn을 곱해주어야 한다.

(이 가중치는 복소평면상에서 단위원 위의 점과 같다. 오일러 공식 eiθ = cosθ + isinθ을 응용한다.)

(파이썬에서는 복소수를 j로 사용한다.)

중복 값을 나눠서 계산하기에, 범위는 N // 2까지만 계산하면 된다.

 

위에서 언급한 FFT와 IFFT가 다른 단 하나의 부분이 이 코드다.

실제로 FFT는 2𝝿jn을 가중치로 사용하지만, IFFT는 -2𝝿jn을 가중치로 사용한다.

(역연산을 취하려면 fourier matrix를 뒤집어야 한다. 이때 -1이라는 값이 등장한다.)

따라서 처음 FFT 함수를 호출할 때, inverse에 1 혹은 -1을 입력받아서 맨 앞에 부호로써 곱해준다.

 

frt = [even[i] + w_N[i] * odd[i] for i in range(N//2)]
bck = [even[i] - w_N[i] * odd[i] for i in range(N//2)]
return frt + bck

두 가지 리스트를 합쳐서 반환하면 끝난다.

본래는 전체 길이(N)만큼 0으로 초기화 한 다음에, index에 맞게 값을 넣어주어야 한다.

하지만 파이썬의 리스트는 + 연산자를 지원해서, 앞뒤의 리스트를 구한 뒤 더해주면 된다.

FFT의 연산 결과(원리)에 의해서 위와 같은 과정을 따라간다.

 

from cmath import exp, pi
import sys
input = sys.stdin.readline
  

def FFT(a: list, inverse: int) -> list:
    N = len(a)
    if N == 1: return a
    
    even = FFT(a[0::2], inverse)
    odd  = FFT(a[1::2], inverse)

    w_N = [exp(inverse*2j*pi*n/N) for n in range(N//2)]
        
    frt = [even[i] + w_N[i] * odd[i] for i in range(N//2)]
    bck = [even[i] - w_N[i] * odd[i] for i in range(N//2)]
    return frt + bck


length = int(input())
N = 1 << length.bit_length() + 1

A = list(map(int, input().split())) * 2   + [0] * (N - length * 2)
B = list(map(int, input().split()))[::-1] + [0] * (N - length)

A_FFT = FFT(A, 1)       # FFT
B_FFT = FFT(B, 1)       # FFT

mul = [A_FFT[l] * B_FFT[l] for l in range(N)]
inverse = FFT(mul, -1)  # IFFT

print(max(round(real_num.real / N) for real_num in inverse))

결과적으로 FFT와 IFFT를 구분하지 않고 하나의 함수로 묶을 수 있었다.

또한, 처음에 받는 리스트의 길이가 2의 제곱수이든 아니든 상관하지 않고 동작할 수 있다.

최대한 간결하고, 정수만 담아서 깔끔하게 작성했다.

무엇보다 열흘의 시간이 한 번에 터지는 그 희열이 엄청났다.

조만간 NTT도 도전할 듯하다.